Elements of Regression
Preface
The goal of these notes is to provide material for a course, Elements of Regression, at the University of Texas at Austin. The main constraint on this course is that there are very limited prerequisites; a course in statistics using R (SDS320E) and/or a course in data science (SDS322E) are the only requirements. This makes finding an appropriate textbook challenging, since this is also supposed to be sufficient for learning how to apply linear regression in research!
One of the things that I have tried to emphasize is the importance of linear regression for prediction and decision making. I place less importance than other sources on making (often dubious) assumptions, as linear regression is often useful when modeling assumptions are not satisfied.
I expect these notes to evolve over time, and am happy to get any feedback from students!
Who This Is For?
Much of the structure and material in this book is inspired by the book’s of John Fox
I am aiming at a slightly lower level of difficulty, however. These books are targeted towards students and researchers in the social sciences. Linear regression is much more broadly useful than this, however: it is applied widely in medicine, computer science, business, biology, physics, and just about any other field that regularly deals with data. Accordingly, I have tried to use examples that cover a wider range than just social sciences.
I have also tried to aim these notes at consumers of data analysis, rather than producers. Most readers will not be data scientists or statisticians professionally, and even those who are may find themselves looking at regressions done by others rather than producing analyses themselves.
What Is Covered?
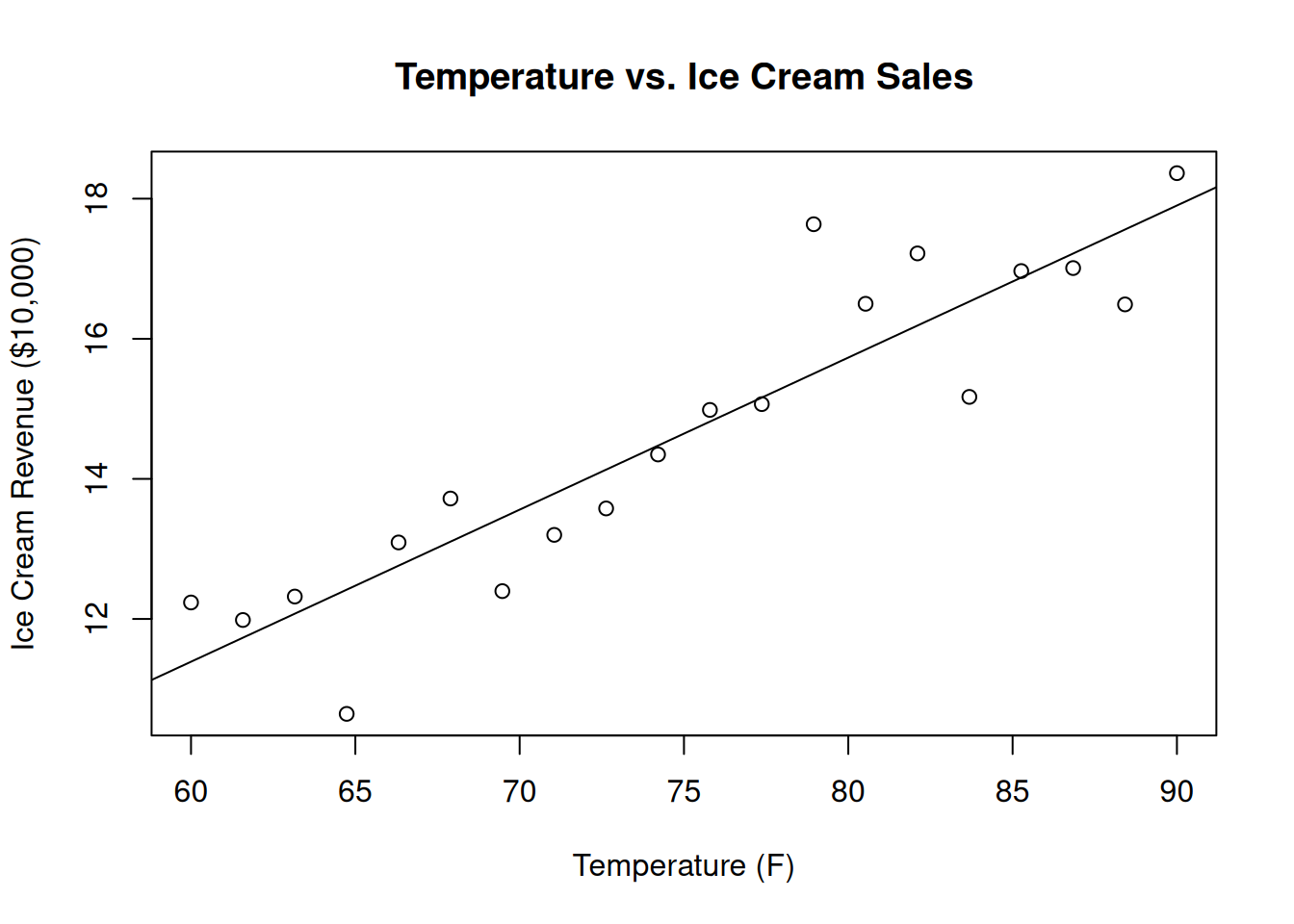
The majority of this course concerns linear regression, with an emphasis on its use in practice to accomplish a variety of common tasks. The picture you should have in your head for what linear regression looks like is something like this:
Given some predictor variable (temperature) we want to predict an outcome (revenue from ice cream sales), and we want to do this using a linear relationship
\[ y = mx + b. \]
This is just the starting point, and we might also want to consider more than one predictor (temperature and distance from the beach), or have the relationship be a bit more complicated (\(y = ax^2 + bx + c\)). Linear regression is capable of dealing with all of these problems.
Examples of some of the problems we will look at include:
Using linear regression to predict future outcomes. For example, I might want to forecast the amount of ice cream I can expect to sell at the beach on a given day so that I know how many materials I should buy, and I would like to use a weather forecast for the following day to make such a prediction.
Using linear regression to determine whether a variable is useful for predicting future outcomes. For example, maybe I am on a college admissions board and I want to know whether or not a student will do well. I might be interested in answering the question: if a student has good high school grades, does their SAT score provide additional information about whether they will do well in college? If I determine that it does not, or that it is only marginally useful, maybe I can get away with ignoring SAT score in the admissions process, or focus on other things instead of SAT score in determining admissions, or not require students to take the SAT entirely. Even if I do not use SAT score in admissions, this type of model might also help guide administrators in identifying students who need additional resources.
Maybe I want to design an intervention or policy where I say, for example, that we should limit some sort of air pollution, because a unit increase in a toxin in the air leads causes the average IQ of individuals in a given neighborhood to be a point lower. This task is tricky because it is attempting to make a causal statement about the effect of a policy, whereas usually statistical methods can only infer an association. That is correlation does not imply causation.
Each of the tasks above is related to the problem of prediction (with the causal setting corresponding to predicting what would happen in a hypothetical world where we exposed individuals to a toxin). In addition to its practical utility, prediction also lies at the heart of the scientific method: we start by specifying a hypothesis about the way the world works, and then use our hypothesis to make a falsifiable prediction about some phenomenon. We then tend to prefer the hypotheses that make good predictions, and ditch the ones that do not.
Towards the end of the course we will also consider some advanced topics that technically extend beyond linear regression. Questions we will consider include:
Linear regression is primarily used to predict numeric variables (heights, ice cream sales, etc). What do we do if we want to predict other sorts of things (someones sex, favorite color, or whether a given picture is a picture of that person)?
What do we do when we want to predict something (say, whether someone has a disease or not) from a very large number of predictors (say, the gene expression levels for every single gene in an individual’s genome)?
Along the way, we will have to deal with a bunch of other issues, such as figuring out whether using a linear regression is a good idea or not (if it’s not, can we fix it?), visualizing our data, running statistical analyses in R, and trying to wrap all of our conclusions within the framework of inferential statistics (using, for example, \(P\)-values and confidence intervals).